Determinación de la tasa libre de riesgo en el costo de capital y la tasa de deuda

#Tasa de interés #Costo de capital #Bono  #Rendimientos esperados  #Tasa libre de riesgo

#Riesgos #Renta Fija #Rendimiento #Inversión #Primas

Autor: Sergio Bravo Orellana

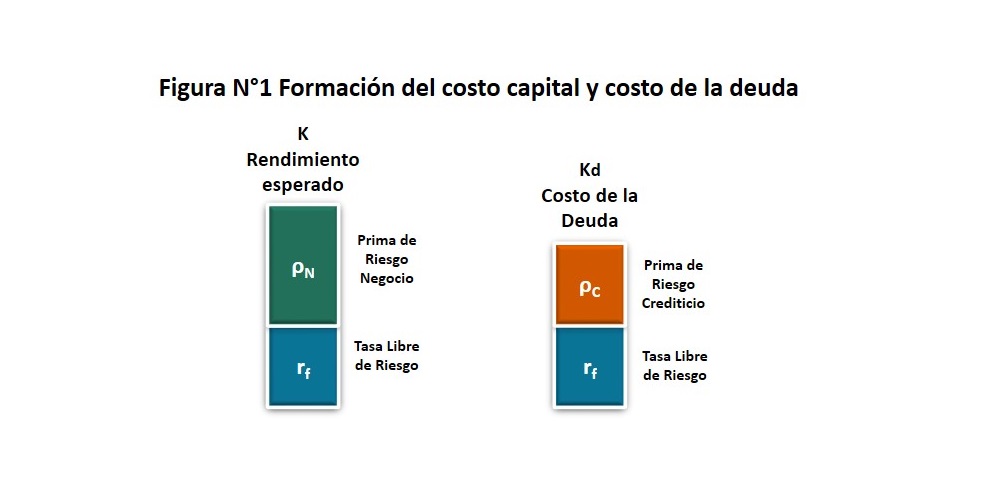
Las tasas de interés y de rendimientos esperados (costos de capital) por los accionistas que se utilizan para evaluar y financiar una determinada inversión, se forman a partir una tasa de referencia que se denominada tasa libre de riesgo. Sobre esta tasa se estima las primas que corresponden a los riesgos de cada negocio y así se encuentra los rendimientos esperados; y en lo que corresponde al costo de la deuda se adiciona la prima por riesgo crediticio.

Con frecuencia, se utiliza el CAPM (Capital Asset Pricing Model) para determinar el rendimiento esperado o costo de capital que utiliza el rendimiento de los bonos de tesoro estadounidense para estimar la tasa libre de riesgo a la cual se añade un spread o prima por el riesgo que corresponde a la inversión realizada conocida como prima de riesgo del negocio. De manera similar ocurre en la formación de la tasa de interés para el financiamiento de esa u otras inversiones, pues el costo de la deuda se forma a partir una tasa de referencia (tasa libre de riesgo) a la cual se suma una prima por riesgo crediticio que incluye el riesgo país, costo de devaluación, los riesgos del emisor y del instrumento de deuda emitido, entre otros factores. Eso se observa en la figura anterior.

Determinación de la tasa libre de riesgo

En la literatura sobre el CAPM, existe un consenso sobre el uso de los rendimientos de los bonos cero-cupón (Zero-Coupon Bond) emitidos por el tesoro estadounidense como la tasa libre de riesgo. Sin embargo, no hay un consenso definitivo sobre la periodicidad del instrumento a utilizar.

 Las posiciones más relevantes al respecto son:

i.                     Utilizar el T-Bill (bono cero-cupón de tres meses o un año) o el T-Bond (bono cero-cupón a 10 años).

ii.                   Estimar el rendimiento utilizando un promedio de largo plazo (40 o 50 años) tomando los T-Bill o T-Bond.

iii.                 Alternativamente se utiliza la tasa spot (la cotización del momento) y generalmente se toma el bono de 10 años.

Ante estas distintas posiciones, para poder uniformizar los conceptos para la determinación del costo de capital se partirá de lo expuesto en el artículo “Comparación del rendimiento de activos financieros de renta fija: La importancia de la duración (duration)”. En este artículo, se trató la importancia del concepto de duración de un activo financiero, el cual es útil para determinar que rendimientos de los instrumentos financieros son equivalentes y comparables. Ahora, se utilizará para uniformizar los rendimientos de las distintas opciones de inversión, ya sea en activos reales o financieros.

La idea de utilizar el concepto de duración para la determinación de la tasa de referencia es parte del hecho de que un proyecto de inversión implica la formación de flujos económicos, en el que se muestra inversiones y flujos de repago en un determinado horizonte de evaluación que resultan en un determinado rendimiento.

Con la información es posible calcular la duración del proyecto, lo que permitirá establecer una equivalencia con un bono cero-cupón, cuyo periodo de redención -o duración- sea el mismo de la duración del proyecto. Esto indica que la tasa de referencia o tasa libre de riesgo a utilizar corresponderá a la tasa de rendimiento de los bonos cero-cupón (Zero-Coupon Bond) emitidos por el tesoro estadounidense que coincida con la duración de los flujos económicos del proyecto.

Para ver si existe la posibilidad de encontrar en todos los casos un bono que coincida exactamente con la duración de los flujos del proyecto es relevante revisar los conceptos de la curva de rendimiento.

La curva de rendimiento

Como se ha mencionado, los bonos más utilizados son los bonos cero-cupón (Zero-Coupon Bond) emitidos por el tesoro estadounidense a tres meses (T-Bill), un año, diez años o treinta años (T-Bonds); mostrando  cada uno distintos rendimientos conforme a su periodo de redención.  Los rendimientos esperados por los inversionistas  al invertir en bonos cero-cupón se forman entre el valor de redención (valor facial del bono) que promete pagar el bono en la fecha de redención y la inversión o pago realizado por dicho bono.

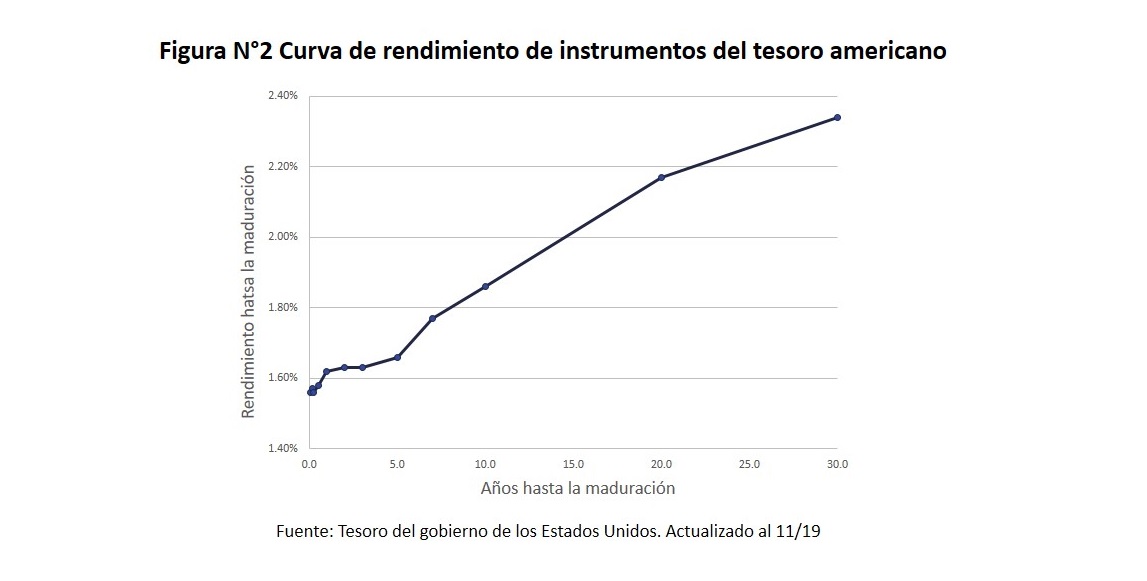
El rendimiento de la inversión dependerá de los plazos de redención del bono, ya que el tiempo es un factor de riesgo que se valora al momento de la inversión.  Esto significa que el rendimiento esperado de un activo financiero a 10 años será mayor al de 1 año, el que su vez será mayor al de 3 meses. Es así como se forma una curva de rendimiento de un activo financiero, como se puede observar en la figura 2, los rendimientos esperados se van incrementando conforme más extenso sea el periodo de redención o maduración del activo financiero.

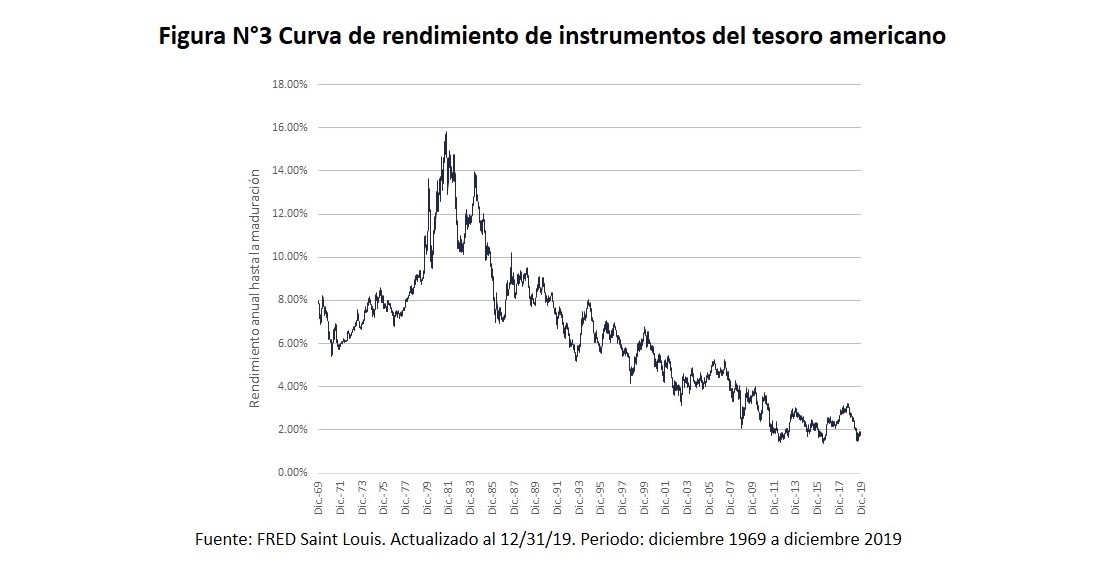
Por otro lado, se debe tomar en cuenta que la curva de rendimiento de un activo financiero es una fotografía en un periodo que puede variar o desplazarse en el tiempo; por ejemplo, puede ser afectada por condiciones económicas del mercado, generando que los rendimientos de los bonos de un mismo emisor (tesoro estadounidense) pueden ser mayores o menores; pero que se mueven en conjunto, es decir la curva se va desplazando.  En la figura 3 se puede observar la evolución de los rendimientos esperados en los últimos 50 años de un bono de 10 años de maduración y que en su evolución refleja los resultados del balance de oferta y demanda del mercado del dinero del momento de la cotización. 

En consecuencia, en una determinada coyuntura económica y financiera se tendrá una curva de rendimiento de la tasa libre de referencia o tasa libre de riesgo a utilizar y que ulteriormente definirán los rendimientos esperados de los accionistas o las tasas de interés.  Para este efecto, los bonos del tesoro estadounidense y sus curvas de rendimiento son útiles, pues representan la base sobre la cual se forman las distintas tasas de rendimiento en los diversos mercados financieros; es decir, son una tasa de referencia global. Por lo que, el costo de capital y la tasa de interés que corresponden a un determinado proyecto de inversión se forman a partir de estos bonos, considerando que correspondan a la misma duración.

Tasas promedio o Tasas spot

Como se mencionó anteriormente, la literatura no es clara sobre qué tasa libre de riesgo utilizar para determinar la tasa base del rendimiento esperado o costo de capital, si utilizar el promedio de largo plazo de los rendimientos históricos de un determinado T-Bill o T-Bond o el rendimiento del momento de la decisión de inversión o tasa spot. La diferencia entre estas tasas puede ser notable, como lo que ocurre en este momento en que las tasas spot están sumamente bajas, y considerar tasas de promedios históricos podría llevar a considerar que una inversión no es rentable a pesar que sus costos de financiamiento son hoy bajo. Y es que la tasa de referencia también determina el costo de la deuda y si como hoy los rendimientos de los bonos estadounidenses y todas las tasas de referencia están en su nivel histórico más bajo, esto implicará la reducción de las tasas de endeudamiento.

La tasa de referencia o tasa libre de riesgo son la base del cálculo de los rendimientos esperados y las tasas de interés de la deuda y este base común hace que están íntimamente relacionados, es decir que ambos crecen o decrecen de acuerdo con el movimiento de la tasa de referencia. Esta relación es relevante, pues el objetivo es el rendimiento de una inversión debería cubrir el costo del financiamiento de la cuál firma parte la deuda, por eso se sostiene que el rendimiento de un proyecto de inversión siempre debería ser mayor a la tasa de interés con la que se ha de financiar.

Entonces, si las tasas de interés se reducen en el mercado, los inversionistas podrán aceptar alternativas de menos rentabilidad pues la lógica es que deban cubrir el costo de la deuda más una prima (spread) que mide la diferencia de riesgo entre el rendimiento esperado de la inversión y el costo de la deuda. Y viceversa, si las tasas de interés se elevan, se dejará de invertir en la menos rentables pues no logran cubrir las nuevas tasas de interés o los nuevos rendimientos esperados construido con tasas más altas.

La lógica descrita es utilizada cuando el gobierno utiliza las tasas de interés como herramienta de política monetaria, pues un incremento en la tasa de interés de referencia desincentiva la inversión, ya que los rendimientos de los proyectos cada vez se vuelven insuficientes para cubrir los mayores rendimientos esperados. Mientras que una política monetario expansiva -reducción de la tasa de referencia-  incentiva la inversión, pues disminuyen los rendimientos esperados y por lo tanto caca vez que caen las tasas hay más proyectos que pueden ejecutarse.  Tal como menciona Donita Rodríguez, la tasa de referencia que establecen los Bancos centrales tiene un efecto de traspaso[1].  

Los proyectos de inversión deben evaluarse considerando las condiciones del momento en que se realiza la inversión; es decir, con los costos de financiamiento, tanto en la deuda como en el rendimiento esperado de los accionistas.  Como se ha mencionado, estas tasas son influenciadas por la tasa de referencia o tasa libre de riesgo y que corresponderá a la tasa spot en cada momento de inversión pues será el momento donde se invierta y se financie el proyecto. La variación de esa tasa spot se puede apreciar en la figura 2, que se ve que en distintos momentos hay tasas de distinto valor, pero también en cada momento se tiene una curva de rendimiento y entonces se debe tener una tasa spot que corresponda a la duración de los flujos económicos de la inversión.

La duración de un bono Cero-Cupón

En el documento “Comparación del rendimiento de activos financieros de renta fija: La importancia de la duración (duration)” se puede apreciar la relación del periodo de redención y maduración de un bono de tesoro estadounidense, estos son iguales para un bono cero-cupón. Entonces si determinamos la maduración de un flujo de repago de la inversión del proyecto entonces podemos elegir un bono cero-cupón de igual maduración -o redención-.

Se podrá percibir que no es lo mismo evaluar un proyecto de inversión con horizontes de 1, 5, 10, 15, 30 años o a perpetuidad, ya que cada inversión tendrá una tasa libre de riesgo distinta, pues los flujos de cada uno de estos proyectos determinarán una maduración distinta y por lo tanto se debería elegir bonos cero-cupón con maduración correspondiente.

El mismo razonamiento es útil para determinar  las tasas de interés de una deuda, pues al sustentarse en la tasa de referencia o tasa libre de riesgo, debería elegirse la tasa libre de riesgo o bono cero-cupón del tesoro estadounidense que corresponda al periodo de maduración del flujo de la deuda.

Determinación de la tasa de referencia del costo de capital de una inversión

Un proyecto de inversión establecerá un flujo económico con las principales inversiones en la etapa preoperativa y sus respectivos flujos de repago en la etapa operativa.

A la vez se debe establecer el horizonte de evaluación del proyecto, que puede definirse según la vida útil del activo principal o cuanto dure el negocio que implica esta inversión, en ambos casos se establece un horizonte de evaluación finito.  En otros esquemas de inversión los horizontes de evaluación son infinitos considerando un esquema de perpetuidades, que es común en la valorización de empresas. Adicionalmente, a las consideraciones anteriores, es importante incluir en el análisis la periodicidad de los flujos de caja (anuales, trimestrales o mensuales).

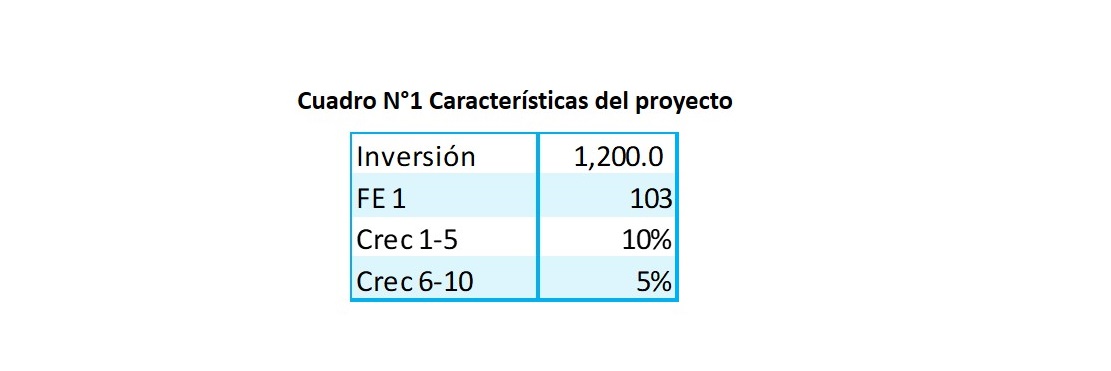
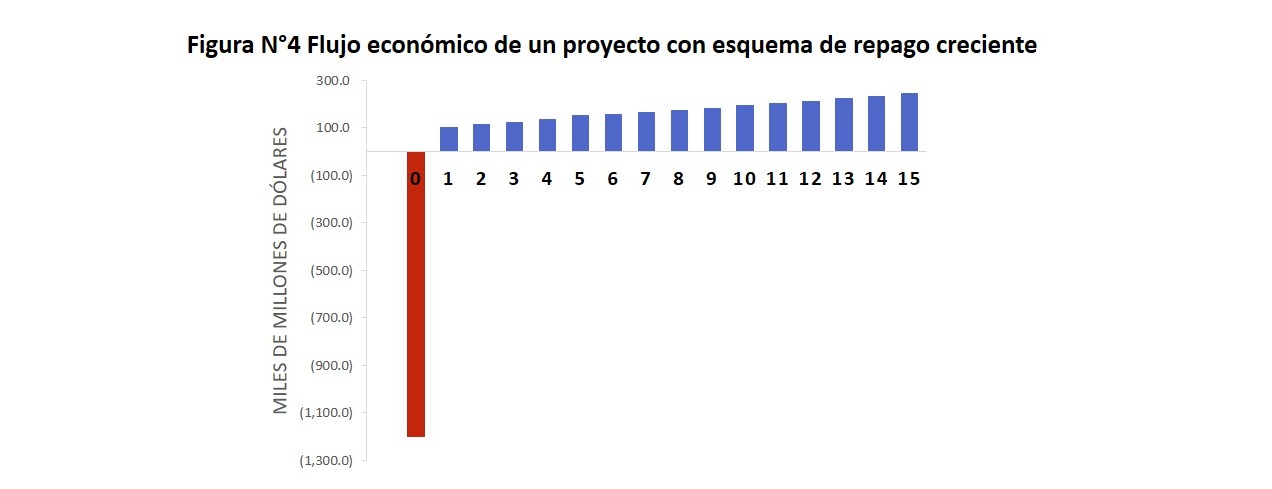
Como ejemplo, se determinará el valor de la tasa de referencia -la tasa libre de riesgo- para un proyecto que tiene las siguientes características: Se realizará una inversión de $1,200 MM que tiene la capacidad de generar el primer flujo económico de $103 MM, con una tasa de crecimiento entre el año 1 y 5 del 10%, luego una tasa de crecimiento del 5% entre el periodo 6 y 15, lo que se resumen en el Cuadro N°1.

Los flujos económicos, que consideran la inversión y el flujo de caja neto del repago de las inversiones se muestran en el Cuadro N°2 , teniendo una inversión de $1,200 MM y un flujo creciente desde el periodo 1 hasta el 15. La tasa interna de retorno esperada (TIR) de esta inversión resulta en 10% . Los flujos también se puede aprecian en la figura siguiente.

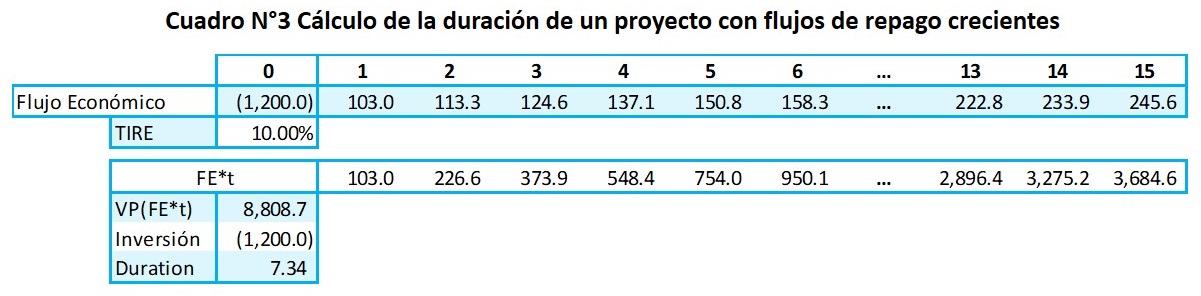
Para calcular la duración del flujo de inversión, se multiplica cada flujo económico por el número del periodo que le corresponde. Así para el periodo 1, tendremos la multiplicación del flujo de $103’ * 1 (igual a 103’) y para el periodo 15, el flujo de 245.6 * 15 (igual a 3,684’6), así para cada periodo. Luego ese flujo ponderado por el número de periodos se actualiza  al momento cero resultando en 8,808’7. Finalmente, la duración resulta de dividir el valor actual del flujo económico ponderado entre la inversión  que equivale a  7.34 años.

En consecuencia, corresponderá buscar como tasa de referencia o tasa libre de riesgo el rendimiento esperado de la deuda americana a una duración de 7.34 años,  ello se debe calcular a partir de la curva de rendimiento presentada en el cuadro N°3, del cual se puede determinar un rendimiento de 1.78%, que correspondería a la tasa libre de riesgo a utilizar en el cálculo del costo de capital o rendimiento esperado mediante el CAPM.

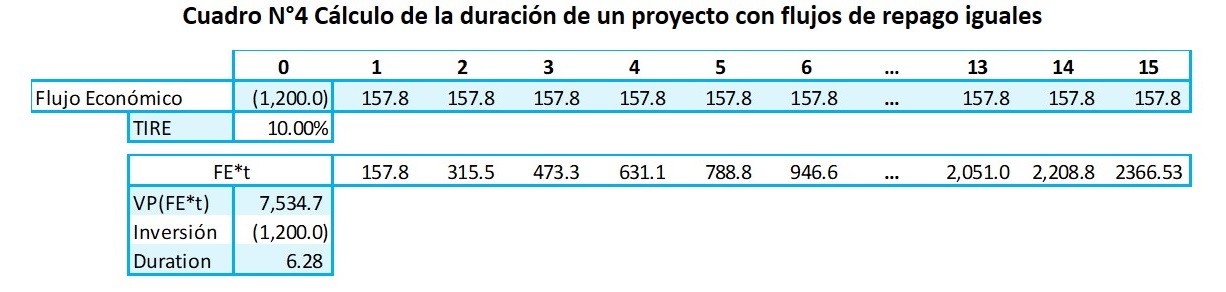
Se debe tener en cuenta que los flujos económicos pueden tener distintas características, algunos que permiten la recuperación de la inversión que otros, inclusive con iguales horizontes de evaluación. Para observarlo se presenta un nuevo formato de los flujos construyendo un esquema de pagos iguales que retribuye la inversión realizada de $1,200 MM, manteniendo el rendimiento del flujo económico en 10% y el periodo de repago en 15 años.

Al realizar el cálculo de la duración de este nuevo esquema de pagos resulta en 6.28 años, menor al 7.34 anterior. Esta reducción de la duración reconoce que en el esquema de pagos iguales se tiene un mayor flujo de repago en el primer periodo ($157.7 MM frente a $103.0 MM) y uno menor  en el último periodo ($157.7 MM frente a $245.6 MM), lo que se refleja en la duración.

Este resultado hace que la tasa de referencia para el esquema de recuperación de la inversión por pagos iguales sea 1.73%; menor frente a 1.78% de un esquema de pagos crecientes.  Se observa que la diferencia significativa; sin embargo, en caso de que el periodo de recuperación fuese 5 años y con un esquema de pagos iguales la diferencia sería más notoria.

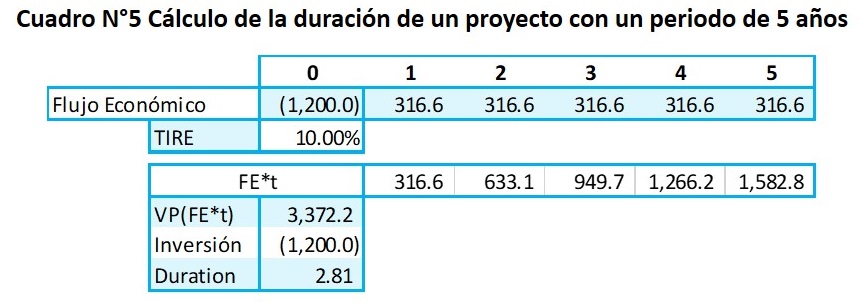
En el siguiente ejemplo, se tiene una inversión de $1,200 MM con un rendimiento del 10% y un periodo de recuperación de 5 años, lo que eleva los flujos de repago a $316.6 MM. Obteniéndose una duración de 2.81 años, el cual es significativamente menor que el 6.28 años.

Esto trae como consecuencia que la tasa de referencia para el esquema de recuperación de la inversión por pagos iguales a 5 años sea 1.63% frente a 1.73% de flujos a 15 años, una diferencia de 0.1%. Esta diferencia si bien no parece significativa como tasa, en términos de valor presente producen diferencias. Y también se debe tomar en cuenta que estamos en un momento donde las tasas de la deuda estadounidense han descendido y las diferencias entre las tasas de corto plazo y largo plazo no son muy grandes como se puede observar en la figura 2, donde la curva de rendimientos muestra una diferencia de 0.8%, pero en otros momentos las diferencias se van ampliando e incrementándose. Entonces las variaciones dependerán del momento de análisis de la inversión.