Comparación del rendimiento de activos financieros de renta fija: La importancia de la duración (duration)

#Duration #Préstamos #Bono  #Banco  #Duración

#Periodo # RentaFija # rendimiento #ActivoFinanciero

Autor: Sergio Bravo Orellana

En el presente artículo, se quiere presentar la influencia del periodo de repago de un préstamo o inversión en un activo financiero, como por ejemplo pagarés o bonos.  Debido a que puede haber instrumentos de deuda o inversión con la misma Tasa Interna de Retorno (TIR). No obstante, ello no significa necesariamente que tienen el mismo rendimiento para los inversionistas o prestamistas.

Para este análisis se tendrán tres posiciones a evaluar, ya sea por un banco o un inversionista en un bono, pues ambos son acreedores y  analizan del mismo modo. En este artículo,  por simplicidad elegiremos el análisis de un préstamo otorgado por un banco.

A modo de ejemplo, el préstamo para evaluar será de $1,000 que deberá repagarse en 5 años. Se establecerán distintas modalidades y todas las alternativas se programarán como la misma tasa de interés del 10%.

Alternativa 1. Préstamo con un servicio de deuda de pagos iguales.

La primera alternativa a evaluar será una programación del servicio de la deuda bajo un formato de pagos iguales. Con los datos anteriores y las fórmulas de Excel se calcularía el servicio de la deuda de la siguiente manera: , el resultado del cálculo establece un pago de $263.8 en cada año de los próximos 5 años, como se muestra en el cuadro 2

Alternativa 2. Préstamo con un servicio de deuda de pagos iguales.

A veces los flujos del negocio a financiar tienen perfiles de flujo de caja creciente y por lo tanto el potencial de repago de la deuda no es alto al inicio. Entonces, la segunda alternativa sería un sistema de pago denominado bullet repayment donde en los primeros periodos se realiza solo el pago de los intereses y al final se amortiza el total del principal, a una tasa de interés del 10%, la programación se visualiza en el cuadro 2.

Alternativa 3. Préstamo con un solo pago al final del periodo de maduración.

Una manera menos utilizada en préstamos, pero aplicable a bonos, es tener un único pago (balloon payment) al final del periodo de maduración (maturity date). Este es el caso de los bonos de cupón cero (zero-coupon bond) en el cual no se realiza pago alguno en los primeros periodos. Considerando una tasa de interés del 10%, la programación se observa en cuadro 2.

Como se puede observar, las tres alternativas de programación de deuda tienen el mismo rendimiento del 10% para el acreedor o inversionista, ya que la tasa de interés con la que se construyeron los servicios de deuda es la misma.  Sin embargo, se pueden plantear las  siguientes preguntas:

• ¿Son alternativas equivalentes para los acreedores o los bonistas?
• ¿Cómo se pueden comparar de manera uniforme estas alternativas?
• ¿Es posible construir programaciones de deuda equivalentes con distintos esquemas de repago?

La intuición sugiere que no son flujos de deuda equivalentes; por ejemplo, en la primera alternativa las amortizaciones y pagos de intereses se reciben desde el primer periodo, lo que disminuye el riesgo de una de pérdida en la colocación por los eventos que puedan ocurrir en el tiempo. En la segunda alternativa, si bien la amortización se posterga hasta el final del periodo de pago los intereses se pagan en cada periodo. En la última alternativa, se tiene un escenario donde la amortización y los intereses del préstamo se pagan al final, lo que incrementa el riesgo de que algún suceso dificulte el repago de la obligación.

El tiempo es una variable importante de riesgo, pues en ese lapso pueden ocurrir cambios en las condiciones financieras -como variación de las tasas de interés- o cambios de posición de solidez o liquidez del emisor.

Un concepto importante en las finanzas es que solamente se pueden comparar rentabilidades de flujos de caja que tienen similar riesgo.  Por lo expresado en el párrafo anterior, las tres alternativas no están al mismo nivel de riesgo.

El concepto y cálculo de la duración (duration) de un instrumento financiero

La duración (duration) de una acreencia -derivado de un préstamo o inversión en bonos- nos brinda dos tipos de información importante:

Primero, nos indica el número equivalente de periodos en el que se recupera una determinada colocación, mediante el cálculo del valor actual ponderado de cada repago correspondiente al servicio de la deuda o a los cupones en el caso de los bonos. Además, en su versión modificada aproxima un factor que calcula la sensibilidad que tiene el valor de la colocación ante una variación de la tasa de interés.

En el flujo de deuda de la primera alternativa  se puede calcular la duración a partir de una simplificación de la fórmula de Macaulay, que expresa que la duración se obtiene de la división entre el valor presente de cada servicio de deuda que es ponderado por el periodo donde ocurre el flujo respectivo VP(SD_i*t_i) y el préstamo de colocación (P) quedando la formula expresada de la siguiente manera  .

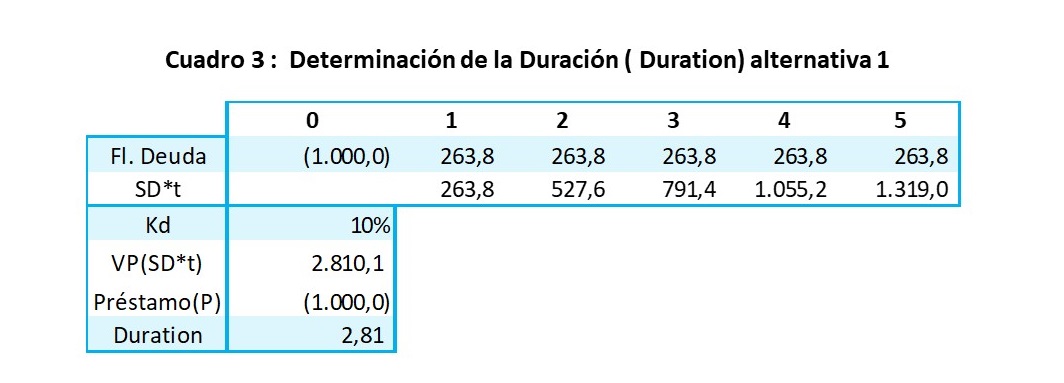Como se puede observar en el flujo de la primera alternativa el valor presente VP(SD_i*t_i) es  $2,810.1 que dividido entre el préstamo (P) de $1,000  da como resultado el periodo de repago de dicha deuda que es igual a  2.81 años. Esto significa que el flujo de deuda sería equivalente a uno donde se paga el principal y los intereses a 2.81 años.

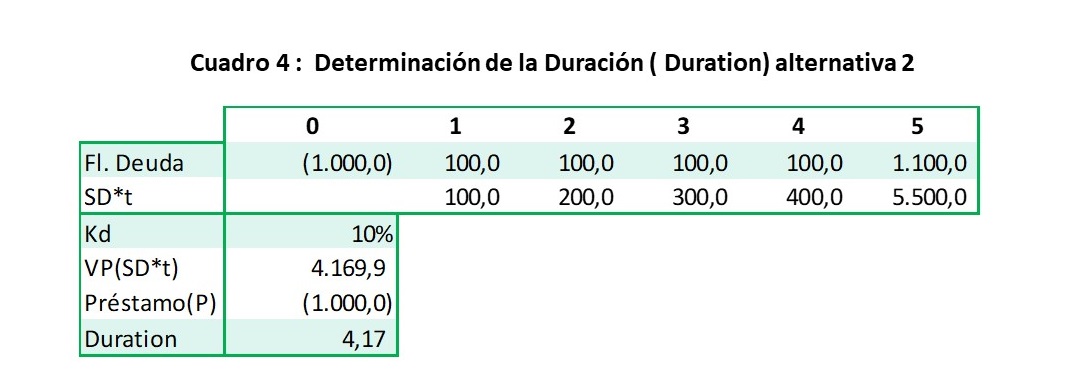
En la segunda alternativa, donde se pagan solamente intereses en los primeros 4 periodos y se amortiza el préstamo al final -con los intereses respectivos-, resulta que VP(SDi*ti) sería $4,169.9, que dividido entre el préstamo (P) de $1,000 da como resultado un periodo de repago equivalente de dicha deuda en 4.17 años. Se observa en este indicador que la primera alternativa tiene un periodo de repago menor que la segunda, por lo tanto, menor riesgo.

Para fortalecer el concepto de la duración de un instrumento financiero, se va a construir activos financieros de similar riesgo considerando la administración del riesgo del tiempo o duración de una acreencia o inversión en un bono.

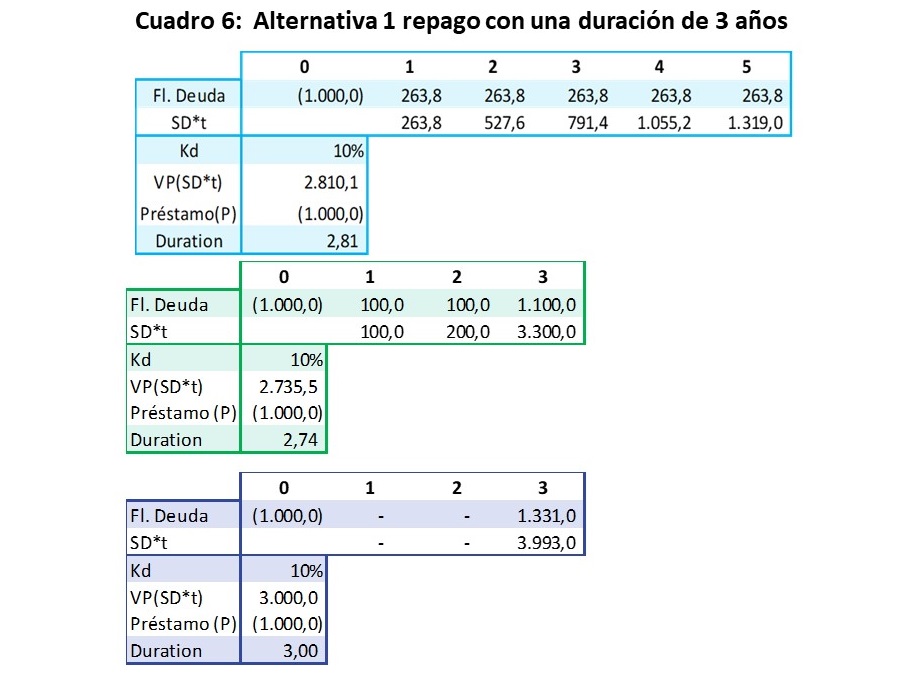
En el análisis de la alternativa 1 se tenía una duración de 2.81 años; es decir, el préstamo se pagaba en un periodo promedio equivalente a 2.81 años, por lo que se podría programar las otras alternativas a 3 años y acercarse a la duración de 2.81 años. En ese escenario, si se mantiene la tasa de interés del 10% se podría programar la deuda con dicha tasa y un repago al final del 3er periodo del principal adicionado a los intereses, obteniéndose como resultado una duración de 2.74 años. Esto significa que se podría adicionar un periodo de repago o modificar la tasa.

Si se programa el repago de la deuda -principal e intereses- al final del 3er periodo,  se tendría una duración de 3.0, lo que significa que se debe reducir el repago a un periodo de 2.81 años. Así pueden surgir múltiples alternativas donde se establecen diversos flujos de repago de la deuda y tasas de interés. Como ejemplo, se propone una programación de deuda de flujos menores en el periodo 1 y 2 (de $100 a $71.8), compensando con un mayor pago en el periodo 3 (de $1,100 a $1,164.7) y manteniendo la tasa del 10%, se puede lograr en una programación de 3 periodos una duración de 2.81 años.

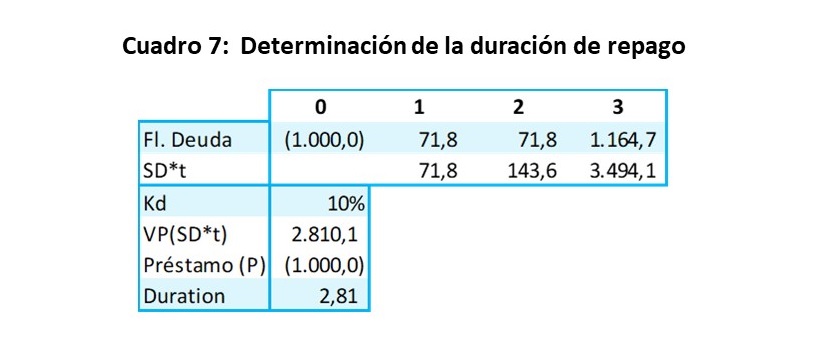De los resultados se puede decir que la programación de la deuda a 3 periodos es equivalente a la de 5 años mediante pagos iguales, manteniendo la tasa de rendimiento o interés del 3%. Como se ha podido observar, el periodo de duración permite trabajar con flujos de distinta naturaleza y programación, también ayuda a evaluar que posiciones son financieramente equivalentes o cuales son superiores o inferiores a otras.

La duración modificada (duration). La sensibilidad de un cambio de tasa de interés

La duración modificada busca encontrar una relación entre el cambio en la tasa de interés y el impacto que se tendría en el valor de los préstamos o del bono. Para ejemplificar, se analizará el cambio de valor de la deuda en el supuesto que en el mercado secundario la tasa de interés se incrementa en 1% (de 10% a 11%). Como se observó líneas arriba, la alternativa 1 se construyó con una tasa de interés (Kd) del 10% y el rendimiento o TIR era igual.

Sin embargo, si se incrementa la tasa de interés, el valor presente del flujo de servicio de deuda para el banco o para los bonistas, se reducirá frente a su valor original; es decir, perderá valor. Si se calcula el valor presente del servicio de la deuda al 11% con la fórmula de actualización siguiente:  P11% = VNA(11%, SD1…SDs), resulta en $975. Entonces, se observa que el valor ha caído en 2.5% respecto a su valor original ( 975/1000-1).

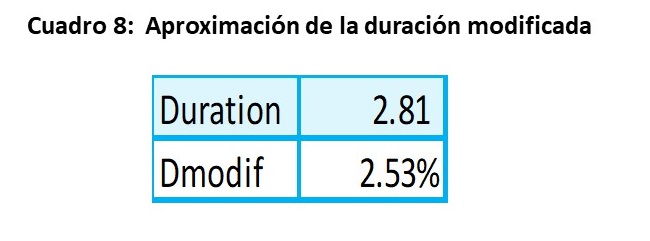
Lo anterior significa que, si la tasa de interés se incrementa en 1%, el valor del activo financiero se reduce en -2.5%. Este mismo resultado se puede aproximar a través del cálculo de la duración modificada, el cual parte del valor de la duración original (2.81) y se calcula con la siguiente relación:  D_modificada=Duración/(1+Kdnuevo)

Esta expresión incluye los valores de la duración y la nueva tasa de interés:  D_modificada = 2.81/(1+11%). El resultado se expresa en porcentaje y resulta en una D_modificada de 2.53%, el cual es un resultado parecido al 2.50% anterior, lo que sígnica que esta fórmula simplificada resulta ser una buena aproximación.

Del mismo modo, si la tasa de interés tiene una caída de 10% a 9%, se puede decir que la acreencia del banco o la inversión de los bonistas incrementa su valor en 2.53%.