El amigo secreto de Navidad: El intercambio de regalos desde la teoría de juegos

Escribe Diego Alonso Quispe Cárdenas, alumno de Economía de la Universidad del Pacífico.

De todas las actividades navideñas, el intercambio de regalos suele ser una de las más populares en círculos de amigos. Usualmente, cuando uno participa en estos intercambios, suele enfrentar algunas dudas ¿Qué pasaría si la persona a la que le toca regalarme no me compra un regalo? ¿Y si compra algo que no me gusta? ¿Cambia mi decisión si me toca jugar con alguien especial a quien voy a ver luego de Navidad? Estas preguntas hacen referencia a las acciones de la persona con la que voy a intercambiar regalos. Esas situaciones, donde uno tiene que pensar en las acciones de los demás para tomar la mejor decisión, son llamadas interacciones estratégicas (Tadelis, 2013). A la descripción formal de estas situaciones se le conoce como “juegos”, y son el centro de estudio de la teoría de juegos. Esta es una herramienta muy útil para la economía, dado que muchas interacciones entre agentes económicos son, en última instancia, juegos (Von Neumann & Morgenstern, 2007).

De este modo, se puede plantear un juego que simule dicha interacción, para ello es conveniente revisar dos conceptos: juego simultáneo y juego de información completa. Por un lado, el intercambio es un juego simultáneo cuando toda vez que los jugadores toman una decisión la hacen sin observar las acciones de los otros jugadores (Tadelis, 2013). Por otro lado, este es de información completa, si los jugadores conocen las preferencias de los demás (Gibbons, 1994). Por ejemplo, un intercambio de regalos donde hay una lista en la cual todos ponen su regalo preferido y el costo, se puede considerar de información completa.

El dilema del intercambio de regalos

Normand y O’Hare (2015) plantearon una versión de un conocido juego que se asemeja a dicho intercambio. Este es un juego simultáneo de información completa, donde cada individuo tiene dos posibles acciones: o comprar o recibir. Si un individuo recibe regalo, obtiene un nivel de satisfacción “S”, y si un individuo compra un regalo, asume un costo de “-C”. Para ser prácticos, asumiremos que la satisfacción de recibir un regalo siempre es mayor al costo de darlo y que los jugadores tienen las mismas preferencias.

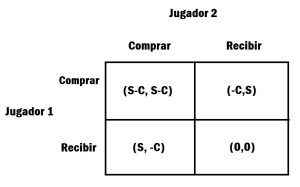
Esta propuesta nos deja con tres tipos de escenarios: En el primero, los dos jugadores compran, es decir, obtienen un beneficio de “S-C”; en el segundo, uno compra y el otro recibe, por lo cual, el que compra solo enfrenta el costo “-C”, mientras que el que recibe obtiene “S” de beneficio; en el tercero, los dos eligen recibir, en otras palabras, ninguno compra regalo, por lo que el beneficio de ambos sería 0. Estos casos pueden representarse gráficamente de la siguiente manera:

Aquí se especifican los resultados, o pagos, de todas las posibles decisiones de ambos jugadores. Dentro de cada paréntesis está primero el pago al jugador 1 y luego el pago al jugador 2. A esta representación gráfica se la conoce como matriz de pagos.

Si bien este juego parece innecesario o irreal, es una versión de uno de los juegos más conocidos: el dilema del prisionero. Adaptaciones de este juego pueden modelar muchas situaciones, entre ellas, las decisiones de producción de empresas con poder de mercado y las decisiones en disputas políticas.

El resultado

Hasta ahora se ha descrito el juego, pero ¿cuál sería la mejor respuesta de cada jugador? Pues que ambos jueguen recibir y no se compre ningún regalo. Esto puede resultar poco intuitivo, ya que ambos jugadores recibirían un mayor pago si ambos compran. Sin embargo, aquí la mejor decisión depende exclusivamente de las posibles decisiones de los otros jugadores. Esta se obtiene cuando cada jugador evalúa qué resultado le da mayor pago, analizando cada decisión del otro. A este resultado se le conoce como equilibrio de Nash, aquella situación donde ambos jugadores juegan su mejor respuesta a la mejor respuesta de su contrincante.

Cabe resaltar que este modelo, a priori, no incluye normas sociales que podrían tener los jugadores; sino que se los toma como individuos que velan solo por sus intereses. Por ello, si se agregan nuevas consideraciones al juego, este equilibrio puede cambiar. Por ejemplo, si el costo de comprar el regalo es 0 o si la satisfacción de recibir el regalo tiende a infinito, el equilibrio cambia (Cornell University, 2017). Así, algunos supuestos se pueden cambiar sin complicar mucho el juego, como la temporalidad o incorporar algunas actitudes sociales.

¿Estrategia a largo plazo o espíritu navideño?

En cuanto al tiempo, si el intercambio de regalos se repetirá las siguientes Navidades con la misma persona, se le añade un componente de memoria al juego, por lo que los jugadores recordarán si se les dio un regalo la Navidad pasada (Cornell University, 2017). Este dilema del prisionero repetido sí permite un equilibrio de Nash donde ambos compren regalos, no obstante, depende de la estrategia escogida por cada jugador.

En lo referido a actitudes, se puede incluir una consideración extra: el espíritu navideño “E”, esto es la satisfacción inherente por comprar un regalo o el placer de regalar (Normand & O’Hare, 2015). Esta consideración puede llegar a cambiar el equilibrio de Nash, ya que, si el espíritu navideño es estrictamente mayor al costo del regalo, se pasaría al caso dónde ambos jugadores compran regalos y los intercambian.

Por lo tanto, la decisión de comprar un regalo esta Navidad, así como las grandes decisiones empresariales y políticas, pueden seguir una misma lógica usando la teoría de juegos. Así, siempre habrá un equilibrio de mejor respuesta que resuelva el juego, aun cuando este no sea evidente. Por último, salvaguardando supuestos y citando equivocadamente a Voltaire, la vida es como un juego, por lo que la teoría de juegos puede ayudarnos a jugarlo un poco mejor.

Referencias

 Tadelis, S. (2013). Game Theory: An introduction. Princeton University Press.

Von Neumann, J., & Morgenstern, O. (2007). Theory of games and economic behavior. Princeton University Press.

Gibbons, R. (1994). A primer in Game Theory. Prentice Hall.

Normand, R. & O’Hare, A. (2015, Diciembre 20).  How to apply Game Theory to buying your Christmas presents. The Conversation in partnership with Stirling University. (en línea).https://theconversation.com/how-to-apply-game-theory-to-buying-your-christmas-presents-52233

Cornell University (2017, Setiembre 11). Gift giving and Game Theory. Networks. Course blog for INFO 2040/CS 2850/Econ 2040/SOC 2090. (en línea). https://blogs.cornell.edu/info2040/2017/09/11/gift-giving-and-game-theory/